I frequently predict proportions (e.g., proportion of year during which a customer is active). This is a regression task because the dependent variables is a float, but the dependent variable is bound between the 0 and 1. Googling around, I had a hard time finding the a good way to model this situation, so I've written here what I think is the most straight forward solution.
Let's get started by importing some libraries for making random data.
from sklearn.datasets import make_regression
import numpy as np
Create random regression data.
rng = np.random.RandomState(0) # fix random state
X, y, coef = make_regression(n_samples=10000,
n_features=100,
n_informative=40,
effective_rank= 15,
random_state=0,
noise=4.0,
bias=100.0,
coef=True)
Shrink down the dependent variable so it's bound between 0 and 1.
y_min = min(y)
y = [i-y_min for i in y] # min value will be 0
y_max = max(y)
y = [i/y_max for i in y] # max value will be 1
Make a quick plot to confirm that the data is bound between 0 and 1.
from matplotlib import pyplot as plt
import seaborn as sns
%matplotlib inline
sns.set_style('whitegrid')
plt.hist(y);
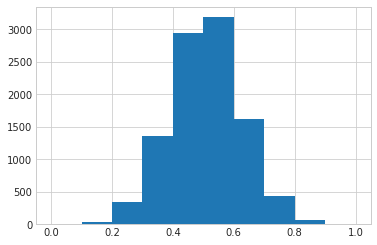
All the data here is fake which worries me, but beggars can't be choosers and this is just a quick example.
Below, I apply a plain GLM to the data. This is what you would expect if you treated this as a plain regression problem
import statsmodels.api as sm
linear_glm = sm.GLM(y, X)
linear_result = linear_glm.fit()
# print(linear_result.summary2()) # too much output for a blog post
Here's the actual values plotted (x-axis) against the predicted values (y-axis). The model does a decent job, but check out the values on the y-axis - the linear model predicts negative values!
plt.plot(y, linear_result.predict(X), 'o', alpha=0.2);
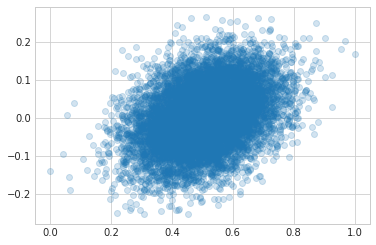
Obviously the linear model above isn't correctly modeling this data since it's guessing values that are impossible.
I followed this tutorial which recommends using a GLM with a logit link and the binomial family. Checking out the statsmodels module reference, we can see the default link for the binomial family is logit.
Below I apply a GLM with a logit link and the binomial family to the data.
binom_glm = sm.GLM(y, X, family=sm.families.Binomial())
binom_results = binom_glm.fit()
#print(binom_results.summary2()) # too much output for a blog post
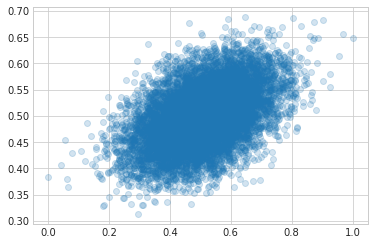
Here's the actual data (x-axis) plotted against teh predicted data. You can see the fit is much better!
plt.plot(y, binom_results.predict(X), 'o', alpha=0.2);
%load_ext watermark
%watermark -v -m -p numpy,matplotlib,sklearn,seaborn,statsmodels
CPython 3.6.3
IPython 6.1.0
numpy 1.13.3
matplotlib 2.0.2
sklearn 0.19.1
seaborn 0.8.0
statsmodels 0.8.0
compiler : GCC 7.2.0
system : Linux
release : 4.13.0-38-generic
machine : x86_64
processor : x86_64
CPU cores : 4
interpreter: 64bit